Our Research
TQM at the Microscale designs unique experiments on quantum spin liquids, topological materials, and high-temperature superconductors in order to understand them at the most fundamental level.
From an applicational standpoint, there is a huge push to further our understanding of quantum spin liquids for example, for the development of topological quantum computing. Conventional approaches to quantum computers rely on local interactions between qubits, but these are prone to interference from the noise of the everyday world. Alternative approaches are based on nonlocal topological excitations, such as Majorana fermions. One route would be through engineering one-dimensional superconducting heterostructures, but it’s unclear how this will scale to larger sizes. A more robust approach would be to find a topological superconductor or spin liquid that intrinsically hosts Majorana excitations, but the correct material has not yet been identified.
In order to find the right material for topological quantum computing or other future technologies, we need to investigate and understand the intrinsic properties of potential candidates. Ideally, new materials are available in any size in high quality. In reality, samples are often only available as powders, 2D materials, or heterostructures, presenting challenges to bulk thermodynamic measurements. Our group focuses on extending the applicability of thermodynamic techniques, such as resonant torsion magnetometry and pulsed echo ultrasound, to the most exciting and challenging materials of tomorrow. One of our group’s main strengths is pushing these techniques to explore materials in the highest magnetic fields—an often unexplored regime where new and technologically-useful states of matter are expected!

WHY QUANTUM MATERIALS?
While all materials are quantum at some level, the phrase ‘quantum materials’ is used when the effects of quantum mechanics determine the material properties. This is what makes their incredible properties useful for major technological advances. Examples include graphene, superconductors, and quantum spin liquids. These quantum materials all exhibit “emergent phenomena”. For example, one electron on its own is a very simple object, but 1023 electrons acting in concert can move with no resistance in a superconductor! As experimental physicists, we face the challenging task of building experiments to track the collective motion of these electrons and come up with a description that allows us to control the design of new materials.

WHY THE MICRON SCALE?
The interesting properties of quantum materials can appear on the macroscale, but their building blocks, like atoms and electrons, live at the nanoscale. The microscale is a fruitful ‘land-in-between’. Sometimes we work at the microscale to tune material properties by changing the size and shape of the sample. Other times, we work at the microscale to enable measurements on samples that are only available in small sizes. For example, exotic materials can be engineered atomic layer by atomic layer with total sample lengths that are limited to just one micron. In order to study these materials, which are too small to work with by hand, advanced microfabrication processes and upgraded measurement methods are needed to extract the right information. We tweak experiments to work for smaller samples, on faster timescales, and with more precision.

WHY THERMODYNAMIC TECHNIQUES?
While it’s impossible, even with today’s computational abilities, to track the individual trajectories of 1023 electrons in a material, thermodynamics provides a workaround. Using statistics of the electrons’ microscopic behaviors, the macroscopic properties of materials can be predicted and directly compared to measurements. This is the power behind thermodynamic techniques — they allow us to connect measurable quantities to microscopic behavior. Many traditional thermodynamic techniques, like heat capacity and magnetization, only work for large, millimeter-sized crystals. By interfacing thermodynamic techniques with micron-sized samples, we can access unexplored physics.

WHY HIGH MAGNETIC FIELDS?
We develop experiments to investigate materials in magnetic fields up to 100 tesla — the largest magnetic field strength that can reliably found in a laboratory. Magnetic fields provide a non-disruptive and reversible way to study electrons in quantum materials. In some sense, they provide a means for simplifying complex material problems as they reduce the degrees of freedom that electrons can explore. This clues us in on the mechanisms responsible for the properties that emerge even in the absence of magnetic field, such as superconductivity or magnetism. Magnetic fields can also induce the formation of new, exotic states of matter that we have never seen before.
Our Techniques
Resonant Torsion

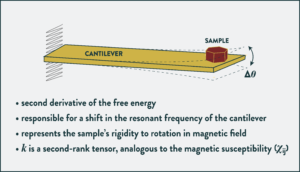
Our workhorse experimental technique is resonant torsion magnetometry. This technique measures a new thermodynamic quantity known as the magnetotropic coefficient — the second derivative of the free energy with respect to magnetic field orientation in the sample. This fact alone makes it ideal for identifying second-order phase transitions; just as other second derivatives of the free energy, including heat capacity, the elastic moduli, or the magnetic susceptibility show sharp discontinuities at phase transitions, so does the magnetotropic coefficient. The magnetotropic coefficient is similar to the magnetic torque in that both are sensitive to magnetic anisotropy. In resonant torsion, a sample mounted onto a cantilever oscillates at the natural frequency of the cantilever. The sample’s magnetic torque, however, is responsible for shifting the equilibrium position about which the lever oscillates. The magnetotropic coefficient leads to a shift in the resonant frequency. The resonant frequency can be measured sensitively both as a function of temperature and magnetic field, allowing the detection of very weak magnetic anisotropy or a signal from very small samples.
Pulsed Echo Ultrasound
 Pulsed echo ultrasound uses a piezoelectric transducer to generate short pulses of sound that travel through the sample. These pulses reflect off the opposite side of the sample and then return to the transducer, generating an electrical signal which is typically amplified and detected on an oscilloscope. With a known path length over which the sound travels, the speed of sound in the material is determined. By measuring the phase of each reflected sound pulse, or “echo”, the change in sound velocity as a function of a parameter like magnetic field or temperature can be measured with better than 1 part in 108 sensitivity. The speed of sound couples to the structural degrees of freedom, but essentially all interactions between electrons on a lattice, such as electron hopping, spin exchange, and coulomb repulsion, depend strongly on the distance between the lattice sites. This introduces couplings between essentially all microscopic degrees of freedom in the material, making ultrasound an ideal probe to study the properties of quantum materials. By measuring the decrease in the amplitude of each successive echo, one obtains the attenuation coefficient—a measure of how easily the sound is absorbed by the material. Varying the measurement frequency allows one to enter interesting regimes where the sound frequency becomes matched to a physical process, such as a relaxation time, and a strong enhancement of the attenuation can clue us in on the mechanisms at play. Traditional pulsed echo requires large millimeter- or even centimeter-sized samples and regular shapes. Our group is currently working to miniaturize this technique with FIB lithography, which enables measurements to higher frequencies on materials that are only available as tiny crystallites.
Pulsed echo ultrasound uses a piezoelectric transducer to generate short pulses of sound that travel through the sample. These pulses reflect off the opposite side of the sample and then return to the transducer, generating an electrical signal which is typically amplified and detected on an oscilloscope. With a known path length over which the sound travels, the speed of sound in the material is determined. By measuring the phase of each reflected sound pulse, or “echo”, the change in sound velocity as a function of a parameter like magnetic field or temperature can be measured with better than 1 part in 108 sensitivity. The speed of sound couples to the structural degrees of freedom, but essentially all interactions between electrons on a lattice, such as electron hopping, spin exchange, and coulomb repulsion, depend strongly on the distance between the lattice sites. This introduces couplings between essentially all microscopic degrees of freedom in the material, making ultrasound an ideal probe to study the properties of quantum materials. By measuring the decrease in the amplitude of each successive echo, one obtains the attenuation coefficient—a measure of how easily the sound is absorbed by the material. Varying the measurement frequency allows one to enter interesting regimes where the sound frequency becomes matched to a physical process, such as a relaxation time, and a strong enhancement of the attenuation can clue us in on the mechanisms at play. Traditional pulsed echo requires large millimeter- or even centimeter-sized samples and regular shapes. Our group is currently working to miniaturize this technique with FIB lithography, which enables measurements to higher frequencies on materials that are only available as tiny crystallites.
Microscale Transport

 Electrical transport is one of the most basic characterization methods. In a standard four-point transport measurement, four wires are used to pass current through the sample and measure the change in voltage to determine the electrical resistivity. In many cases, single crystals are only available with dimensions too small to squeeze four wires onto the sample by hand. In addition to sample constraints, there are many reasons that miniaturizing transport can be very beneficial; using FIB lithography, the placement of the electrical contacts can be chosen precisely in order to measure the anisotropy within a single device or to detect both longitudinal and Hall resistivity at the same time. The ability to finely tune the geometry and size of the sample itself can be used to increase the signal sizes to measure highly-conductive samples, especially at high magnetic fields where small samples reduce eddy current heating. In fact, microscale transport is highly compatible with pulsed magnetic fields, where the very rapidly changing magnetic field strength can induce voltages and electrical noise into the measurement. Because wires can be tightly twisted all the way to the point of contact on the sample, open loop areas are reduced and sensitivity is improved. We use this high sensitivity to directly measure the electronic structure of metals and observe field-temperature scaling in cuprate superconductors.
Electrical transport is one of the most basic characterization methods. In a standard four-point transport measurement, four wires are used to pass current through the sample and measure the change in voltage to determine the electrical resistivity. In many cases, single crystals are only available with dimensions too small to squeeze four wires onto the sample by hand. In addition to sample constraints, there are many reasons that miniaturizing transport can be very beneficial; using FIB lithography, the placement of the electrical contacts can be chosen precisely in order to measure the anisotropy within a single device or to detect both longitudinal and Hall resistivity at the same time. The ability to finely tune the geometry and size of the sample itself can be used to increase the signal sizes to measure highly-conductive samples, especially at high magnetic fields where small samples reduce eddy current heating. In fact, microscale transport is highly compatible with pulsed magnetic fields, where the very rapidly changing magnetic field strength can induce voltages and electrical noise into the measurement. Because wires can be tightly twisted all the way to the point of contact on the sample, open loop areas are reduced and sensitivity is improved. We use this high sensitivity to directly measure the electronic structure of metals and observe field-temperature scaling in cuprate superconductors.


